Niveaux d’énergie d’un atome

I. Structure de l’atome

L’atome est composé d’un noyau central constitué de protons, portant une charge positive \( +e \) (où \( e = 1,602 \times 10^{-19} \, C \)), et de neutrons, neutres électriquement. Autour du noyau gravitent des électrons, chacun portant une charge négative \( -e \), et répartis sur des niveaux d’énergie définis, appelés couches électroniques. Chaque couche correspond à une certaine énergie potentielle de l’électron par rapport au noyau.

II. Quantification des niveaux d’énergie

Les niveaux d’énergie des électrons sont quantifiés. Selon le modèle de Bohr pour l’atome d’hydrogène, l’énergie d’un électron sur une orbite \( n \) est donnée par : \[ E_n = – \frac{13,6 \, \text{eV}}{n^2} \] où \( n \) est le numéro quantique principal (n = 1, 2, 3, …). Cela signifie que l’électron ne peut pas occuper une énergie intermédiaire entre deux niveaux. Plus \( n \) est grand, plus l’énergie est proche de zéro, ce qui correspond à une position plus éloignée du noyau.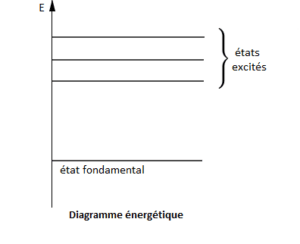  

III. Absorption et émission de lumière

Lorsqu’un électron absorbe de l’énergie (souvent sous forme de photon), il peut sauter vers un niveau d’énergie supérieur, passant d’un état d’énergie \( E_i \) à \( E_j \). La différence d’énergie est reliée à la fréquence \( \nu \) du photon par la relation de Planck : \[ \Delta E = E_j – E_i = h \nu \] où \( h = 6,626 \times 10^{-34} \, \text{J} \cdot \text{s} \) est la constante de Planck. Lorsque l’électron retourne à un niveau inférieur, il émet un photon de même énergie.

IV. Spectres d’émission et d’absorption

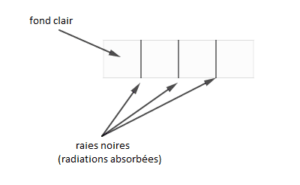
Les spectres d’émission et d’absorption sont spécifiques à chaque élément chimique. Lorsqu’un atome est excité et que ses électrons reviennent à leur état fondamental, ils émettent des photons, produisant des spectres d’émission sous forme de raies colorées sur un fond noir. En absorption, l’atome absorbe certaines longueurs d’onde précises, donnant un spectre avec des raies sombres sur un fond coloré. Chaque spectre est unique, permettant l’identification d’éléments (principe de la spectroscopie).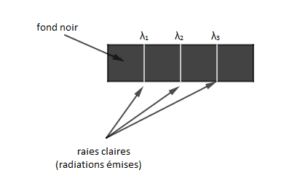  

Le spectre d’émission est constitué par des rayonnements fins clairs sur un fond noir  

Le spectre d’absorption est caractérisé par des rayonnements sombres, sur un fond clair

V. Applications des niveaux d’énergie dans les technologies modernes

Les transitions entre niveaux d’énergie sont essentielles pour des technologies telles que :

• Lasers : générés par des transitions contrôlées d’électrons dans un état excité vers un état inférieur, émettant de la lumière cohérente.
• Écrans LCD : reposent sur des changements d’état moléculaire activés par les niveaux d’énergie électronique.
• Capteurs solaires : utilisent des matériaux semi-conducteurs pour absorber la lumière et produire des électrons.

Les diagrammes énergétiques représentent ces niveaux, illustrant les états fondamentaux et excités.

Exercice d’application

On considère un atome de mercure dont quelques niveaux d’énergie ont pour valeur :

• \( E_3 = -2.72 \, \text{eV} \)
• \( E_2 = -3.75 \, \text{eV} \)
• \( E_1 = -4.99 \, \text{eV} \)
• \( E_0 = -10.45 \, \text{eV} \) (niveau fondamental)

Questions

1. Calculer les énergies des photons émis par l’atome de mercure lorsque celui-ci passe du niveau \( E_3 \) au niveau \( E_1 \) et du niveau \( E_2 \) au niveau \( E_0 \).
2. Quelles sont les longueurs d’onde \( \lambda_{3,1} \) et \( \lambda_{2,0} \) des rayonnements émis ? Dans quels domaines de radiations se trouvent ces deux longueurs d’onde ?

Résolution

1) Calcul des énergies des photons

Soit \( E_{n,p} \) l’énergie du photon émis lorsque l’atome passe d’un niveau \( n \) d’énergie \( E_n \) à un niveau \( p \) d’énergie \( E_p \) avec \( E_p < E_n \). Pour la transition du niveau 3 au niveau 1, on a : \( E_{3,1} = E_3 – E_1 \) Application numérique : \( E_{3,1} = -2.72 \, \text{eV} + 4.99 \, \text{eV} = 2.27 \, \text{eV} \) D’où, \( E_{3,1} = 2.27 \, \text{eV} \). De la même manière, pour la transition du niveau 2 au niveau 0, on a : \( E_{2,0} = E_2 – E_0 \) Application numérique : \( E_{2,0} = -3.75 \, \text{eV} + 10.45 \, \text{eV} = 6.70 \, \text{eV} \) Donc, \( E_{2,0} = 6.70 \, \text{eV} \).

2) Calcul des longueurs d’onde

L’énergie d’un photon est reliée à la longueur d’onde par la relation : \( E_{n,p} = \frac{hc}{\lambda_{n,p}} \), soit \( \lambda_{n,p} = \frac{hc}{E_{n,p}} \) Application numérique pour \( \lambda_{3,1} \) : \( \lambda_{3,1} = \frac{6.62 \times 10^{-34} \times 3 \times 10^8}{2.27 \times 1.6 \times 10^{-19}} = 5.48 \times 10^{-7} \, \text{m} \) D’où, \( \lambda_{3,1} = 548 \, \text{nm} \). Étant donné que \( 400 \, \text{nm} < \lambda_{3,1} < 800 \, \text{nm} \), cette radiation fait partie du domaine du visible, le vert (500 nm < \( \lambda_{3,1} \) < 570 nm). De même, pour \( \lambda_{2,0} \) : Application numérique : \( \lambda_{2,0} = \frac{6.62 \times 10^{-34} \times 3 \times 10^8}{6.70 \times 1.6 \times 10^{-19}} = 1.86 \times 10^{-7} \, \text{m} \) Ainsi, \( \lambda_{2,0} = 186 \, \text{nm} \). Comme \( \lambda_{2,0} < 400 \, \text{nm} \), cette radiation appartient au domaine de l’ultraviolet.